WIEN2k TOPはこちら

 

Q1: LAPW、APW+loとは何ですか？

近年、SlaterのAPW 法を拡張したLAPW法が開発され、2001年にはSchwarzらにより新しいAPW+lo法が示されました。

LAPW法

線形化補強平面波(LAPW)法は、結晶の電子構造を計算するための最も精度の高い手法の一つで、電子の交換・相関相互項を局所スピン密度近似(LSDA)等により表わす、密度汎関数理論に基づいています。これまで複数のLSDAポテンシャルが利用されてきましたが、最近では、一般化密度勾配近似(GGA)を 用いる改良法がよく利用されています。原子価の電子状態には、スカラー相対論(Koelling and Harmon 77)またはスピン軌道相互作用を含む第二変分法(Macdonald 80, Novak 97)により、相対論の効果を取り入れることができます。なお、内殻電子は、完全に相対論的に扱うことができます(Desclaux 69)。

SlaterによるAPW法を線形化したLAPW法のプログラミングに関する手引きは多くの文献で解説がなされています。(Andersen 73, 75, Koelling 72, Koelling and Arbman 75, Wimmer et al. 81, Weinert 81, Weinert et al. 82, Blaha and Schwarz 83, Blaha et al. 85, Wei et al. 85, Mattheiss and Hamann 86, Jansen and Freeman 84, Schwarz and Blaha 96) D. Singh(Singh 94)による優れた書籍では、LAPW法について詳細な解説がなされており、この手法に関心のある研究者にとって有益でしょう。LAPW法の詳細はこれらの成書に譲ることにし、ここでは、基本的な概念を要約するだけにとどめます。

多くの“エネルギーバンド法”がそうであるように、LAPW法は、コーン-シャム方程式を解くための一つの手法であり、結晶の電子状態を記述するのに適した基底系を導入することで、基底状態の電子密度、全エネルギー、多電子系の(コーン-シャム)固有値(エネルギーバンド)を求めることができます。

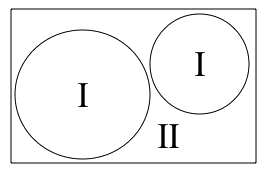
図1：ユニットセルの分割、原子球(I)と格子間領域(II)

 

LAPW法は、ユニットセルを(I)重なりのない原子球(原子位置に中心をもつ)と(II)格子間領域に分割することにより実現され、これら2つの領域において、異なる基底系を用います。

 

(I)半径 Rt の原子球 t の内部を、動径波動関数 Rt と球面調和関数 Ylm(r) の積の線形結合で表します(前後関係から明らかな場合は t を省略します)。

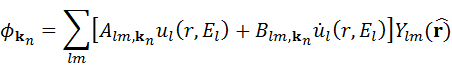
ここで、 ul(r,El) は、エネルギー El (通常、l的な性質をもつバンドの中央のエネルギーが選ばれます)と原子球 t 内部のポテンシャルの球対称部分をもつ動径シュレーディンガー方程式の(原点での)正則解です。 dot ul は、同じエネルギー El で与えられる ul のエネルギー微分です。これら二つの関数の線形結合が、動径関数の線形化を構成しています。 係数 Alm と Blm は、 kn に依存する関数になり(下記参照)、基底関数がそれぞれの平面波(PW)に対応する格子間領域の基底関数に適合する(値と傾き)という要請によって決定されます。 ul と dot ul は、球内部の動径方向のメッシュを用いた、動径波動関数の数値積分により求められます。

 

(II)格子間領域では、平面波基底が用いられます。

ここで、 kn=k+Kn であり、 Kn は逆格子ベクトル、また k は、第1ブリルアンゾーン内の波数ベクトルになります。各平面波は、全ての原子球内において、atomic-likeな関数により補強されています。

このようなLAPWを結合した基底系を用いて、(linear)変分法にしたがい、 Kohn-Sham方程式を解きます。

係数 cn は、Rayleigh-Ritz(変分原理)法により決まります。この基底系の収束は、カットオフパラメータ RmtKmax= 6 – 9 により制御されます。ここで、 Rmt は、ユニットセル内の最小原子球半径、 Kmax は、式(2.6)の K ベクトルの最大値(大きさ)です。

線形化を改良するため(基底の柔軟性をあげる)、またセミコアと価電子を一つのエネルギー枠で扱えるようにするため(直交性を保証)、基底関数( kn に非依存)を追加することができます。この基底は、”ローカルオービタル(local orbitals)” (Singh 91)と呼ばれ、異なる 2つのエネルギー(例えば、 3s と 4s エネルギー)による、2つの動径波動関数、および1つの(いずれか一方のエネルギーにおける)動径波動関数のエネルギー微分の線形結合によって表わされます。

係数 Alm 、 Blm 、および Clm は、 φLO が規格化され、原子球の境界で傾きと値がゼロになるという要請から決定されます。

 

APW+lo 法

Sjöstedt, Nordström と Singh (2000)らは、原子球面上で、平面波の値と傾きをそろえるという余分な制約を伴う標準的なLAPW法は、SlaterのAPW法を線形化する最も効率のよい方法ではないということを示しました。 標準的なAPW基底を用いれば、計算効率は良いです。但し、線形固有値問題として解くために、エネルギーが El に固定された ul(r,El) を用います。そして、動径基底関数に十分な柔軟性を持たせるために新しいローカルオービタル( lo )を追加します。

この新しい lo (2.7式のLOと区別するため小文字で記述)は、従来の”LAPW”基底系と同じような形をしていますが、 kn には非依存で、 Alm および Blm は、原子球の境界で lo が0になり、規格化されるという条件から求められます。

このようにして、原子球の境界に”キンク(kinks/ねじれ)”を持つ基底関数を構築します。そして、それはハミルトニアンの運動エネルギーの部分に表面の項を含むことを要求します。注意、ただし、全波動関数は滑らかに接続され、微分可能である必要があります

Madsen et al. (2001)により示されたこの新しいスキームは、事実上LAPW法と同一の結果に収束します。しかし、“RKmax”の値を小さくことができ、少ない基底系(最大50%)で計算できるため、計算時間を大幅に短縮することができます(最大一桁)。 1つの計算の中で、“LAPW および APW+lo”基底を同時に利用でき、異なる原子、または同じ原子の l ごとに、別々の基底を用いることができます。(Madsen et al. 2001) 一般に、遷移金属の3d状態のように平面波の数を増やしても収束の遅い軌道や小さな原子球を持つ原子の軌道に対して、 APW+lo基底を用い、そうでない軌道にはLAPW基底を用います。 また、セミコアと価電子帯を同時に記述するために、異なるエネルギーによる第2の“LO”を加えることもできます。

 

概論

一般的な形式では、LAPW法は、ポテンシャルを次の形で展開します。

これは、電荷密度も同様です。球対称近似を利用していないため、この手続きは、しばしば“フルポテンシャル”法と呼ばれます。

従来のバンド計算で使われていた“マフィンティン”近似は、 (2.10)の最初の式において、 L=0 と M=0 の成分のみ、また第二式では、 K=0 のみの成分を保持することに相当します。この(旧式の)手続きは、球の内部では球状平均を、また格子間領域では体積平均をとることに相当します。

全エネルギーは、Weinert et al. 82にしたがって計算されます。

ハートリー原子単位が使われる原子関連のプログラム(LSTARTとLCORE)および一部のサブルーチン(LAPW1, LAPW2)を除いて、内部的にはリドベルグ原子単位を採用しています。なお出力は、常にリドベルグ単位で与えられます。

原子の力は、Yu et al (91)にしたがって計算されます。 WIENの実装形式は、Kohler et al (94) and Madsen et al. 2001を参照してください。 Soler and Williams (89)による別の形式も、既に検証されており、計算効率や数値精度において、等価であることがわかっています(Krimmel et al 94)。

改良された四面体法(Bloechl et al. 94)、ガウシアンブロードニングまたは温度ブロードニング法を使用し、フェルミエネルギーと各バンド状態の重みを計算することができます。

基底にスカラー相対論的な固有関数を用いた第二変分法により、スピン軌道相互作用を扱うことができます (MacDonald 80, Singh 94 and Novak 97を参照)。 スカラー相対論的な基底( p3/2 に対応)において、 p1/2 を失った動径基底関数の問題に対処するため、 p1/2 ローカルオービタル、すなわち、 p1/2 基底によるLO、を追加し、標準LAPW基底を拡張しました。これらは、第二変分法によるスピン軌道相互作用(SO)計算で利用できます(Kunes et al. 2001)。

電子が局在している場合(ランタニドの4f状態、幾つかの遷移金属酸化物の3d状態など)、 LDA(GGA)法は、十分な精度を持たないことはよく知られています。この問題に対処するため、各種LDA+U法および“軌道分極(OP)法”が実装されています (Novak 2001 and references thereinを参照)。

外部磁場(Novak 2001を参照)または外部電場(スーバーセルアプローチ, Stahn et al. 2000を参照) による相互作用を考慮することができます。

プロパティ

Blöchl et al. 94による改良されたテトラへドロン法を使用し、状態密度(DOS)を計算できます。

フェルミの黄金率と双極子の行列要素(コア、価電子、電導バンド帯間)により X線吸収および蛍光スペクトルを計算できます(Neckel et al. 75)。

電荷密度のフーリエ変換によりX線構造因子が得られます。

Ambrosch et al. 95,Abt et al. 94, Abt 97および特にAmbrosch 06による個々の双極子の行列要素を修正した“結合状態密度(Joint density of states)” を用いて、光学特性が得られます。また、Kramers-Kronig変換も可能です。

J. Sofo and J. Fuhr (2001)によるプログラムを用いて、 Bader’s “atoms in molecules”理論に基づいた電子密度の解析を行うことができます。

---

 

引用文献

• Abt R., Ambrosch-Draxl C. and Knoll P. 1994 Physica B 194-196
• Abt R. 1997 PhD Theses, Univ.Graz
• Andersen O.K. 1973 Solid State Commun. 13, 133
• — 1975 Phys. Rev. B 12, 3060
• Ambrosch-Draxl C., Majewski J. A., Vogl P., and Leising G. 1995, PRB 51 9668
• Blaha P. and Schwarz K. 1983 Int. J. Quantum Chem. XXIII, 1535
• Blaha P., Schwarz K., and Herzig P 1985 Phys. Rev. Lett. 54, 1192
• Blaha P., Schwarz K., Sorantin P.I. and Trickey S.B. 1990 Comp. Phys. Commun. 59, 399
• Blo”chl P.E., Jepsen O. and Andersen O.K. 1994, Phys. Rev B 49, 16223
• Desclaux J.P. 1969 Comp. Phys. Commun. 1, 216; note that the actual code we use is an apparently unpublished relativistic version of the non-relativistic code described in this paper. Though this code is widely circulated, we have been unable to find a formal reference for it.
• — 1975 Comp. Phys. Commun. 9, 31; this paper contains much of the Dirac-Fock treatment used in Desclaux’s relativistic LSDA code.
• Jansen H.J.F. and Freeman A.J. 1984 Phys. Rev. B 30, 561
• — 1986 Phys. Rev. B 33, 8629
• Koelling D.D. 1972 J. Phys. Chem. Solids 33, 1335
• Koelling D.D. and Arbman G.O. 1975 J.Phys. F: Met. Phys. 5, 2041
• Koelling D.D. and Harmon B.N. 1977 J. Phys. C: Sol. St. Phys. 10, 3107
• Kohler B., Wilke S., Scheffler M., Kouba R. and Ambrosch-Draxl C. 1996 Comp.Phys.Commun. 94, 31
• Krimmel H.G., Ehmann J., Elsa”sser C., Fa”hnle M. and Soler J.M. 1994, Phys.Rev. B50, 8846
• Kunes( J, Nova’k P., Schmid R., Blaha P. and Schwarz K. 2001, Phys. Rev. B64, 153102
• MacDonald A. H., Pickett, W. E. and Koelling, D. D. 1980 J. Phys. C 13, 2675
• Madsen G. K. H., Blaha P, Schwarz K, Sjo”stedt E and Nordstro”m L 2001, Phys. Rev. B
• Mattheiss L.F. and Hamann D.R. 1986 Phys. Rev. B 33, 823
• Neckel A., Schwarz K., Eibler R. and Rastl P. 1975 Microchim.Acta, Suppl.6, 257
• Novak P. 1997 to be published, see also $WIENROOT/SRC/novak_lecture_on_spinorbit.ps
• Nova’k P. , Boucher F., Gressier P., Blaha P. and Schwarz K. 2001 Phys. Rev. B 63, 235114
• Schwarz K. and Blaha P.: Lecture Notes in Chemistry 67, 139 (1996)
• Schwarz K., P.Blaha and Madsen, G. K. H. 2001 Comp.Phys.Commun.
• Singh D. 1991, Phys.Rev. B43, 6388
• Singh D. 1994, Plane waves, pseudopotentials and the LAPW method, Kluwer Academic
• Sjo”stedt E, Nordstro”m L and Singh D. J. 2000 Solid State Commun. 114, 15
• Sofo J and Fuhr J 2001: $WIENROOT/SRC/aim_sofo_notes.ps
• Soler J.M. and Williams A.R. 1989, Phys.Rev. B40, 1560
• Stahn J, Pietsch U, Blaha P and Schwarz K. 2001, Phys.Rev. B63, 165205
• Wei S.H., Krakauer H., and Weinert M. 1985 Phys. Rev. B 32, 7792
• Weinert M. 1981 J. Math. Phys. 22, 2433
• Weinert M., Wimmer E., and Freeman A.J. 1982 Phys. Rev. B26, 4571
• Wimmer E., Krakauer H., Weinert M., and Freeman A.J. 1981 Phys. Rev. B24, 864
• Yu R., Singh D. and Krakauer H. 1991, Phys.Rev. B43, 6411

 

Q2: WIEN2kの技術情報・サポートはどこで入手できますか？

開発元(ウィーン工科大)により、メーリングリストが運営されています。デベロッパを含め、活発な情報交換が行われており、また過去の情報をウェブブラウザから検索することもできます。詳しくは、WIEN2k-Mailing Listをご覧ください。

 

Q3: ポテンシャルを可視化することができますか？

はい、可能です。まず、テキストエディタで case.in0 のNR2VをR2Vに書き換えます。その後、lapw0を実行し、各ポテンシャルをファイルに書き出します。

$ x lapw0

次のコマンドにより、 lapw5.def ファイルを生成します。

$ x lapw5 -d

生成された lapw5.def ファイルの該当箇所(9行目、11行目)をデフォルトの価電子密度(case.clmval)から書き換えます。

 

価電子密度 case.clmval(デフォルト)

クーロンポテンシャル case.vcoul

交換相関ポテンシャル case.r2v

全ポテンシャル case.vtotal

※全電子密度(case.clmsum)の場合、 case.in5 において VAL を TOT に変更

 

lapw5.defの例(case.vtotal)

5 ,'case.in5', 'old', 'formatted',0
6 ,'case.output5', 'unknown','formatted',0
8 ,'case.struct', 'old', 'formatted',0
9 ,'case.vtotal', 'old', 'formatted',0
10,'case.tmp', 'unknown','unformatted',0
11,'case.vtotaldn', 'unknown','formatted',0
12,'case.sigma', 'unknown','formatted',0
20,'case.rho_onedim','unknown','formatted',0
21,'case.rho', 'unknown','formatted',0

変更後、次のコマンドを実行し、case.in5で指定した面の値を取得します。

$ lapw5 lapw5.defcase.in5 の例

1 1 1 2 # プロット中心 (1/2,1/2,1/2)
3 0 1 2 # X端座標 (3/2,0/1/2)
0 3 1 2 # Y端座標 (0,3/2,1/2)
3 3 3 # 描画対象とする原子配置の数
100 100 # グリッド数 (100 x 100 行列)
RHO NO # RHO/DIFF/OVER、ADD/SUB/NO(またはブランク)
ATU VAL DEBU # ATU/ANG、VAL/TOT、DEBU/NODEBUG
NONORTHO # ORTHO/NONORTH

 

case.rhoファイルが生成されるので、rhoplotを使用し可視化します。

$ rhoplot
#####################################
# #
# RHOPLOT #
# #
#####################################
3D- or Contour-plot ? (3/c)3
.4972776316139147
Wait until graph appears. Then press RETURN to continue
contour for surfaces are drawn in 21 levels on grid base
as linear segments
21 incremental levels starting at 0, step 0.1, end 2
contour line types are varied & labeled with format '%8.3g'
Do you want to set ranges? (y/N)y
zmin = (0.0) -30
zmax = (2.0) 10
delta z = (0.1) 1
Wait until graph appears. Then press RETURN to continue
contour for surfaces are drawn in 41 levels on grid base
as linear segments
41 incremental levels starting at -30, step 1, end 10
contour line types are varied & labeled with format '%8.3g'
Do you want to set ranges? (y/N)
Do you want a hardcopy? (y/N)

 

以下、出力例です。

 

(2008/08/29)

 

Q4: XCrySDenを用いてバンド分散図用のk点メッシュを作成する方法は？

基本的な操作は、次のとおりです。

 

1. xcrysdenを起動します。

 

2. Fileメニューから Open WIEN2k… -> Select k-path をクリックします。

 

3. Choose WIEN2k case directory ダイアログが表示されるので、 Selction: に該当するディレクトリ(case.structを含む)を指定し、OKボタンをクリックします。

 

4. ブラベ格子が正しく認識されたことを確認し、 Close ボタンを押し、先へ進めます。

空間群毎のブリルアンゾーンやk点ラベルは、Bilbao Crystallographic Server Table of Space Group Symbolsで確認することができます。

w2web から XCrySDen を起動した場合、上の画面が最初に表示されます。

 

5. ブリルアンゾーンが表示されるので、その中の点(special points)を順次選択していきます。

 

6. 選択が終わると、 OK ボタンを押し、次に進みます。

 

7. 各k点座標を整数比で表わすための係数Mが表示されます。

 

8. Total number of k-points along the path に発生させるk点の数を入力します。この例では、100を指定しました。

 

9. 指定した経路でk点が補間され、klistが作成されます。

 

10. ファイル名をcase.klist_bandとして保存します。

 

w2webからXCrySDenを起動した場合は、一旦xcrysden.klistとして保存し、その後、メニューに従いcase.klist_bandとして複製してください。

 

 

11.最後に履歴が表示されます。

 

(2008/08/29)

 

Q5: 波動関数を可視化することができますか？

はい、LAPW基底であれば可能です。LAPW1で求めたcase.vector[up/dn]を使用し、k点およびバンドの一組で表される波動関数をプロットすることができます。手順は、次のとおりです。

 

0. データフォーマット変換プログラムのビルド

1. case.in1[c]でLAPW基底を指定(※APW+lo未サポートのため)

2. lapw1の実行

3. case.in7の作成

4. lapw7の実行

5. gnuplut用データフォーマット変換プログラムを実行

6. gnuplotを用いて可視化

 

以下、具体的な手順です。

 

0. まず、データフォーマット変換プログラムをビルドします。

 

ソースコード格納ディレクトリ
$WIENROOT/SRC_lapw7/DOC_psink/w1gpl.f ※1Dデータ用
$WIENROOT/SRC_lapw7/DOC_psink/w2gpl.f ※2Dデータ用

 

コンパイル例(g77使用)

$ g77 -o w1gpl w1gpl.f
$ g77 -o w2gpl w2gpl.f

 

コンパイルした各モジュールは、$WIENROOTディレクトリへコピーしてください。

$ cp w?gpl $WIENROOT

 

1. case.in1[c]でLAPW基底(0)を指定します。

 

以下、設定例になります。(赤色文字部分)

WFFIL (WFPRI, SUPWF)

7.00 10 4 (R-MT*K-MAX; MAX L IN WF, V-NMT

0.30 5 0 (GLOBAL E-PARAMETER WITH n OTHER CHOICES, global APW/LAPW)

0 0.30 0.000 CONT0

0 -4.35 0.005 STOP0

1 -2.58 0.010 CONT0

1 0.30 0.000 CONT0

2 0.30 0.010 CONT0

0.30 3 0 (GLOBAL E-PARAMETER WITH n OTHER CHOICES, global APW/LAPW)

0 -1.16 0.010 CONT0

0 0.30 0.000 CONT0

1 0.30 0.000 CONT0

K-VECTORS FROM UNIT:4 -9.0 2.0 24 emin/emax/nband

 

2. つづけて、lapw1を実行し、case.vectorファイルを生成します。

 

スピン分極、complex計算時は適宜オプションを追加してください。

$ x lapw1

 

3. lapw7用入力ファイル case.in7 を作成します。

 

テンプレートは用意されておりませんので、テキストエディタ等で直接作成する必要があります。作成したファイルは、case.in7として保存してください。(※再利用する場合、$WIENROOT/SRC_templatesへコピーしておくと便利です

 

(2D用入力データサンプル)

2D ORTHO
0 0 0 2
3 0 0 2
0 0 3 2
76 76 25 25
NO
RE ANG LARGE
1 0

 

(1D用入力データサンプル)

1D ORTHO
0 0 0 2
4 4 0 2
101 25
NO
IM ANG LARGE
1 0

 

(case.in7の設定内容)

 

次元(0D/1D/2D/3D) 平面を直角(ORTHOGONAL)/非直角(NON-ORTHOGONALまたは空白)

平面の原点座標(X0 Y0 Z0 分母)

平面のX端(X1 Y1 Z1 分母)

平面のY端(X2 Y2 Z2 分母)※1Dでは不要

グリッド数(X方向 Y方向 X増分 Y増分)※1DではY成分不要

ポスト処理(NO/DEP)

出力スイッチ(※1 下記参照) 単位(ANG/AU) 相対論項(LARGE/SMALL)

波動ベクトル(case.klist参照) バンド指数 ※どちらも0とすると全ての値を採用

 

※1 波動関数の出力スイッチ

 

“RE ” リアルパート

“IM ” イマジナリパート

“ABS” 絶対値

“ARG” 複素平面の偏角

“PSI” 複素数

 

4. つづいて、lapw7を実行します。

$ x lapw7

正常に動作すれば、case.psinkファイル(テキストデータ)が生成されます。

 

5. gnuplot用データフォーマット変換プログラムを実行します。

 

手順 0. でビルドしたプログラムを使用し、case.psinkをgnuplot用の形式へ変換します。

 

1次元データの場合

$ w1gpl < case.psink > case.gpl

2次元データの場合

$ w2gpl < case.psink > case.gpl

 

6. gnuplot を用いて可視化します。

$ gnuplot case.gpl

実行後、画像ファイル psi.ps が生成されます。
以下は、fcc-TiN(a=4.235)を対象に上記入力ファイル(case.in7)を用いて描画したサンプルです。

 

(2009/01/09)

 

Q6: CIF(Crystallographic Information File)形式のファイルを取り込めますか？

はい、可能です。

w2web上で新規セッションを開始し、structgenを実行すると、 WIEN2k標準テンプレートを使用するか、cif形式またはxyzを使用するか尋ねられます。
ここで、cifファイルをアップロードし、structファイルへ変換することができます。

 

w2webからのインポートに失敗する場合、コマンドラインからcif2struct の直接実行をお試しください。読み込みに失敗した行の情報が出力されるので、これを修正することで問題を回避することができます。

 

(2009/06/26)

 

Q7: Local DOSを足し合わせてもTotal DOSにならないのですが、理由は何でしょう？

格子間領域(interstital region)のLocal DOSを足し合わせてみてください。TETRA用入力ファイルcase.intにおいて、原子番号を指定するところで、原子数+1の値を指定ください。原子数が2の場合は3、8の場合は9のように。 例えば、TiCの場合(セル内に2原子)、次のように指定します。

$ cat TiC.int
Title
-0.50 0.002 1.500 0.003 EMIN, DE, EMAX, Gauss-broadening(>de)
4 NUMBER OF DOS-CASES specified below
0 1 total atom, case=column in qtl-header, label
1 1 Ti tot
2 1 C tot
3 1 interstitial

(2009/10/01)

 

Q8: フェルミ面を可視化することができますか？

はい、XCrySDenを利用することで容易に行えます。

 

操作方法は、次の通りです。

まず、XCrySDenを起動し、FileメニューからOpen WIEN2k… -> Fermi Surfaceを選択します。

 

ダイアログが表示されるので、WIEN2kのセッションディレクトリを指定します。

 

以下のような、WIEN2k制御用ダイアログが表示されます。k-meshを増やす場合は、Number of k-points:の値を増やし、Generate k-meshをクリックしk-meshを更新してください。続けて、Calculate Eigenvalues [x lapw1]ボタン、Calculate Fermi energy [x lapw2 -fermi]ボタンとクリックします。計算がエラーなく終了すれば、Render Fermi Surfaceボタンをクリックします。

 

Fermi Energyを指定するダイアログが表示されるので、値を確認し、OKボタンをクリックします。

 

新たに3つのウィンドウが表示されます(Band widths, BARGraph, Select bands)。Select bandsにおいて、フェルミレベルに状態を持つバンドのチェックボックスを有効にし、Selectedボタンをクリックします。

 

 

新しいウィンドウが開かれ、フェルミ面が表示されます。

 

 

(2010/08/02)